[지연/week5] 트리의 구현과 순회

트리의 개념

트리는 노드로 이루어진 자료 구조

1. 트리는 하나의 루트 노드를 갖는다.
2. 루트 노드는 0개 이상의 자식 노드를 가지고 있다.
3. 그 자식 노드 또한 0개 이상의 자식 노드를 가지고 있고, 이는 반복적으로 정의된다.

트리는 노드(node)들과 노드들을 연결하는 간선(edge)로 구성되어있다.

• 트리에는 사이클(cycle)이 존재할 수 없다.
• 노드들은 특정 순서로 나열될 수도 있고 그럴 수 없을 수도 있다.
• 각 노드는 부모 노드로의 연결이 있을수도 있고 없을 수도 있다.
• 각 노드는 어떤 자료형으로도 표현 가능하다.

  class Node{
    public String name;
    public Node[] children;
  }
  

• 비선형 자료구조로 계층적 관계를 표현한다. ex) 디렉터리구조, 조직도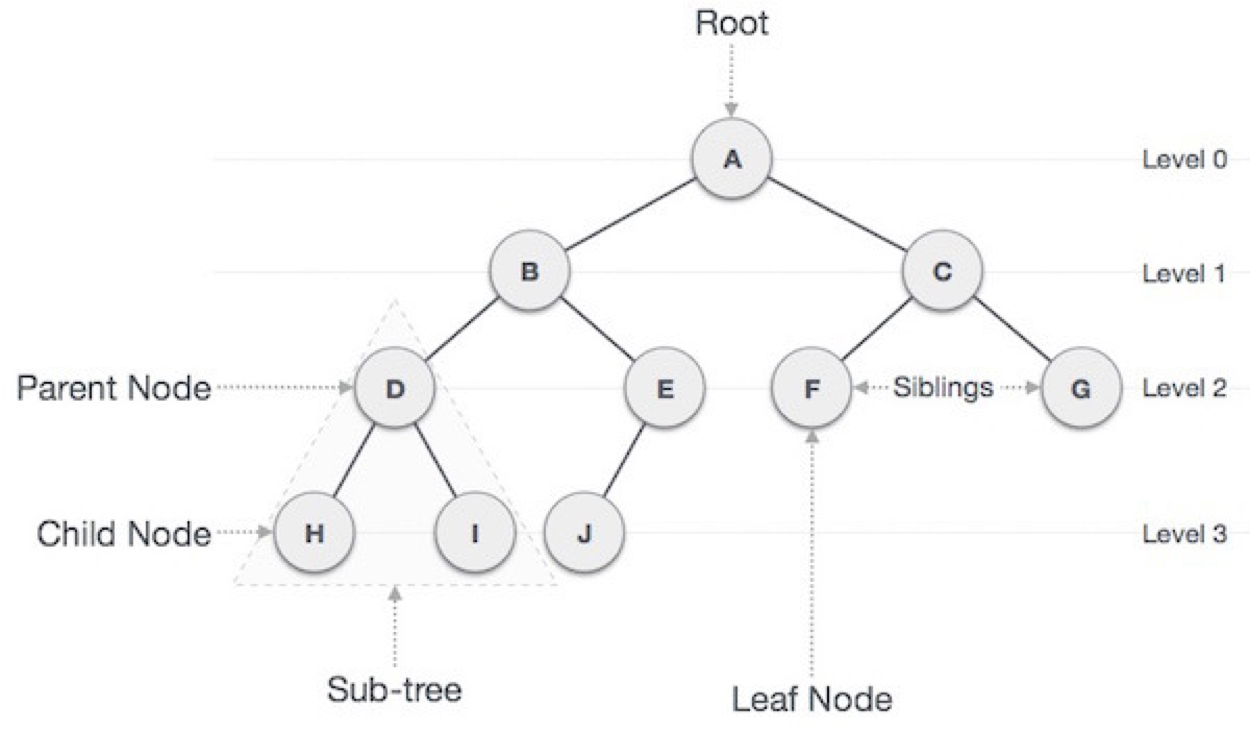
• 그래프의 한 종류다.
  • 사이클이 없는 하나의 연결 그래프
  • 또는 DAG(Directed Acyclic Graph, 방향성이 있는 비순환 그래프)의 한종류이다.

트리와 관련된 용어

• 루트 노드 (root node) : 제일 최고 부모 노드. 트리는 하나의 루트노드만을 가진다.
• 단말 노드 (leaf node) : 자식이 없는 노드. ‘말단 노드’ 또는 ‘잎 노드’ 라고도 불린다.
• 내부 (internal) 노드 : 단말 노드가 아닌 노드
• 간선(edge) : 노드를 연결하는 선 (link, branch라고도 부른다.)
• 형제 (sibiling) : 같은 부모를 가지는 노드
• 노드의 크기 (size) : 자신을 포함한 모든 자손 노드의 개수
• 노드의 깊이 (depth) : 루트에서 어떤 노드에 도달하기 위해 거쳐야하는 간선의 수
• 노드의 레벨 (level) : 트리의 특정 깊이를 가지는 노드의 집합
• 노드의 차수 (degree) : 하위 트리 개수 / 간선 수 (degree) = 각 노드가 지닌 가지의 수
• 트리의 차수 (degree of tree) : 트리의 최대 차수
• 트리의 높이 (height) : 루트 노드에서 가장 깊숙히 있는 노드의 깊이

트리(Tree)의 특징

• 그래프의 한 종류다. 최소 연결 트리 라고도 불린다.
• 트리는 계층 모델 이다.
• 트리는 DAG(Directed Acyclic Graphs, 방향성이 있는 비순환 그래프)의 한종류이다.
  • loop나 circuit이 없다. 즉, 사이클이 없다.
• 노드가 N개인 트리는 항상 N-1개의 간선(edge)를 가진다.
• 루트에서 어떤 노드로 가는 경로는 유일하다.
  • 임의의 두 노드간의 경로도 유일하다.
• 한 개의 루트 노드만이 존재하며 모든 자식 노드는 한 개의 부모 노드만을 가진다.
• 순회는 Pre-order, In-order, Post-order로 이루어진다. 이 세가지 모두 DFS/BFS 안에 있다.
• 트리는 이진트리, 이진탐색트리, 균형트리(AVL트리, red-black트리), 이진 힙(최대 힙, 최소 힙) 등이 있다.

트리(Tree)의 종류

이진트리

• 각 노드가 최대 두개의 자식을 가지는 트리
• 모든 트리가 이진트리는 아니다.

순회의 종류

순회는 재귀(Recursion)으로 구현한다!!

1. 전위 순회 (pre-order traversal)
   • 현재 노드 -> 왼쪽 가지 -> 오른쪽 가지

     void preOrderTraversal(TreeNode node){
      if(node != null){
        visit(node);
        preOrderTraversal(node.left);
        preOrderTraversal(node.right);
      }
     }
     

2. 중위 순회 (in-order traversal)
   • 왼쪽 가지 -> 현재 노드 -> 오른쪽 가지

     void inOrderTraversal(TreeNode node){
      if(node!=null){
        inOrderTraversal(node.left);
        visit(node);
        inOrderTraversal(node.right);
      }
     }
     

3. 후위 순회 (post-order traversal)
   • 왼쪽 가지 -> 오른쪽 가지 -> 현재 노드

     void postOrderTraversal(TreeNode node){
      if(node != null){
        postOrderTraversal(node.left);
        postOrderTraversal(node.right);
        visit(node);
      }
     }
     

이진 탐색 트리 (Binary Search Tree)

• 모든 노드가 아래의 순서를따르는 속성이 있는 이진 트리다.
• 모든 노드 왼쪽 자식들 <= n < 모든 오른쪽 자식들 (모든 노드 n에 대해서 반드시 참)

균형 트리

• O(logN) 시간에 Insert와 find를 할 수 있을 정도로 균형이 잘 잡혀있는 경우
• ex) 레드-블랙 트리, AVL 트리

완전 이진 트리 vs 전 이진 트리 vs 포화 이진 트리

1. 완전 이진 트리 (Complete Binary Tree)

• 트리의 모든 높이에서 노드가 꽉 차있는 이진 트리. 즉, 마지막 레벨을 제외하고 모든 레벨이 완전히 채워져있다.
• 마지막 레벨은 꽉 차있지 않아도 되지만 노드가 왼쪽에서 오른쪽으로 채워져야 한다.
• 마지막 레벨 h에서 (1 ~ 2h-1) 개의 노드를 가질 수 있다.
• 또 다른 정의는 가장 오른쪽 잎 노드가 (아마도 모두) 제거된 포화 이진 트리다.
• 완전 이진 트리는 배열을 사용해 효율적으로 표현 가능하다.

2. 전 이진트리 (Full Binary Tree 또는 Strictly Binary Tree)

• 모든 노드가 0개 또는 2개의 자식 노드를 갖는 트리

3. 포화 이진 트리 (Perfect Binary Tree)

• 전 이진 트리이면서 완전 이진 트리인 경우
• 모든 말단 노드는 같은 높이에 있어야 하며, 마지막 단계에서 노드의 개수가 최대가 되어야 한다.
• 모든 내부 노드는 두 개의 자식 노드를 가진다.
• 모든 말단 노드가 동일한 깊이 또는 레벨을 갖는다.
• 노드의 개수가 정확히 2^(k-1)개여야 한다. (k : 트리의 높이) -> 흔하게 나타나는 경우가 아니다. 즉, 이진 트리가 모두 포화 이진 트리일 것이라고 생각하지 않는다.

이진 힙 (최소 힙과 최대 힙)

1. 최소 힙 (Min Heap)

• 트리의 마지막 단계에서 오른쪽 부분을 뺀 나머지 부분이 가득 채워져있는 완전 이진 트리이며, 각 노드의 원소가 자식들의 원소보다 작다.
  • 즉, key(부모 노드) >= key(자식 노드)인 완전 이진 트리.
  • 가장 큰 값은 루트 노드이다.
  • N개가 힙에 들어가 있으면 높이는 log(N)이다.

2. 최대 힙 (Max Heap)

• 원소가 내림차순으로 정렬되어 있다는 점에서만 최소힙과 다르다.
• 각 노드의 원소가 자식들의 원소보다 크다.

트라이(Trie ; ‘접두사 트리(Prefix Tree’라고도 부른다.)

• n차 트리(n-ary Tree)의 변종
• 각 노드에 문자를 저장하는 자료구조
• 따라서 트리를 아래쪽으로 순회하면 단어 하나가 나온다.
• 접두사를 빠르게 찾아보기 위한 흔한 방식으로, 모든 언어를 트라이에 저장해 놓는 방식이 있다.
• 유효한 단어 집합을 이용하는 많은 문제들은 트라이를 통해 최적화할 수 있다.

트리(Tree)의 구현 방법

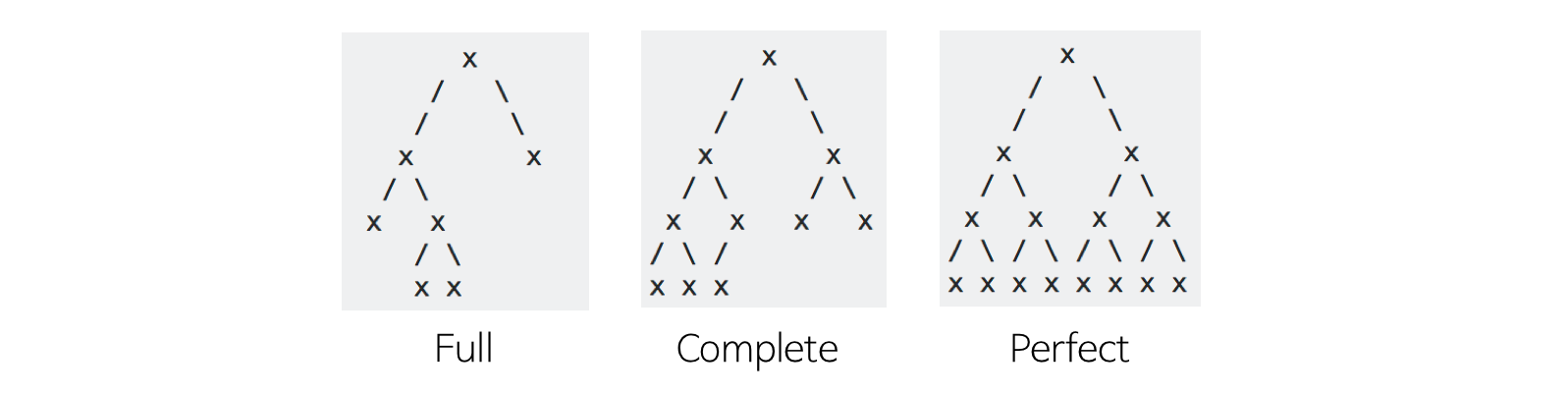
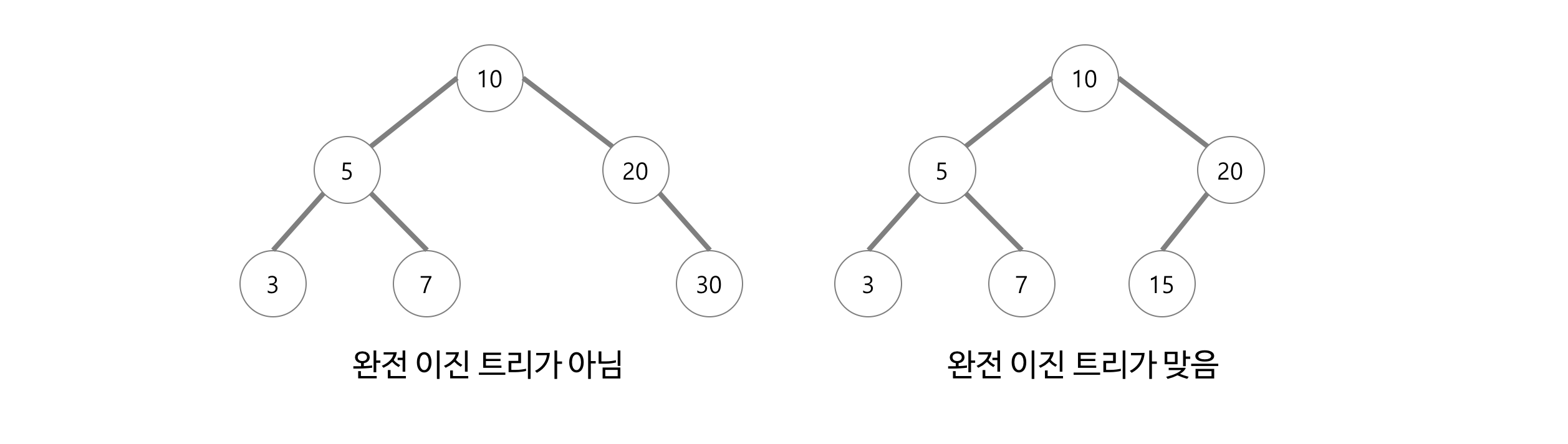
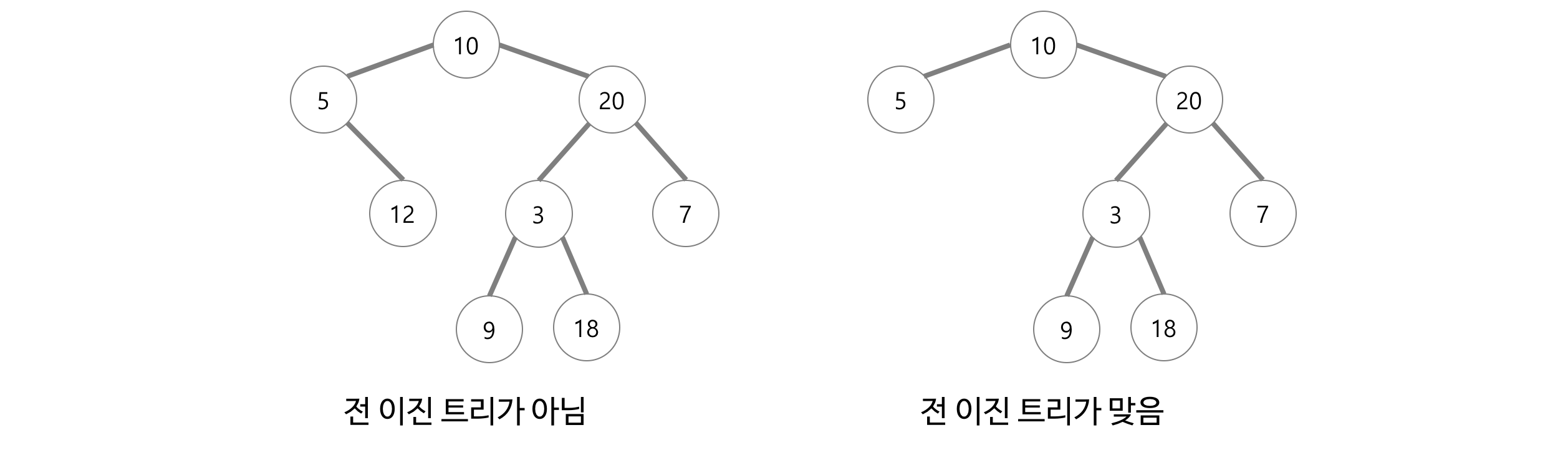
기본적으로 트리는 그래프의 한 종류이므로 구현 방법(인접 리스트 또는 인접 배열)으로 구현할 수 있다.

1. 인접 배열 이용

1. 1차원 배열에 자신의 부모노드만 저장하는 방법
   • 트리는 부모 노드를 0개 또는 1개를 가지기 때문
   • 부모 노드를 0개 : 루트 노드
2. 이진 트리의 경우, 2차원 배열에 자식 노드를 저장하는 방법
   • 이진 트리는 각 노드가 최대 두 개의 자식을 갖는 트리이기 때문
   • ex) A[i][0] : 왼쪽 자식 노드, A[i][1] : 오른쪽 자식 노드

2. 인접 리스트 이용

1. 가중치가 없는 트리의 경우
   • ArrayList<ArrayList> list = new ArrayList<>();
2. 가중치가 있는 트리의 경우
   • 1) class Node {int num, dist; //노드 번호, 거리} 정의
   • 2) ArrayList[] list = new ArrayList[정점의 수 + 1];

그래프의 트리의 차이

Reference

• https://codingstarter.tistory.com/8?category=935492

• 2019 14